【CSP-S 2019】树上的数

2025-12-16

#算法

题目（带图解和三组测试数据，在这个网址 https://uoj.ac/problem/490）：

给定一个大小为 n 的树，它共有 n 个结点与 n−1 条边，结点从 1 ∼ n 编号。初始时每个结点上都有一个 1 ∼ n 的数字，且每个 1 ∼ n 的数字都只在恰好一个结点上出现。

接下来你需要进行恰好 n−1 次删边操作，每次操作你需要选一条未被删去的边，此时这条边所连接的两个结点上的数字将会交换，然后这条边将被删去。

n−1 次操作过后，所有的边都将被删去。此时，按数字从小到大的顺序，将数字 $1 \sim n$ 所在的结点编号依次排列，就得到一个结点编号的排列 $P_i$。现在请你求出，在最优操作方案下能得到的字典序最小的 $P_i$。

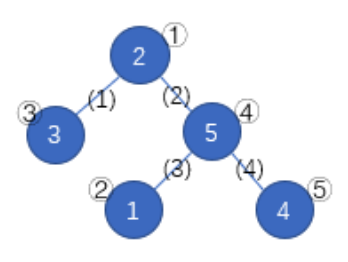
树上的数1

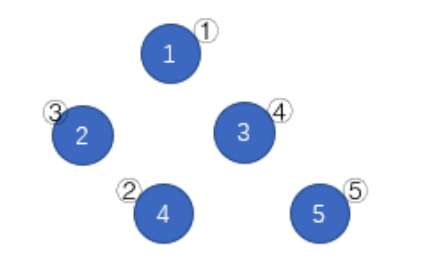
如上图,蓝圈中的数字 $1 \sim 5$ 一开始分别在结点②、①、③、⑤、④。按照 (1)(4)(3)(2)的顺序删去所有边,树变为下图。按数字顺序得到的结点编号排列为①、③、④、②、⑤。排列是所有可能的结果中字典序最小的。

树上的数2

搜到一份代码，这个代码是用：DFS + 并查集 + 节点的出度/入度检查。树的两个节点间的双向的边被编号成两个虚拟节点来判断。对里面的dfs()函数里的下面两处剪枝不太理解：

    if (find(x) == find(y) && size[find(x)] <= adj[x].size()) {
      legal = false;
    }

    if (find(a) == find(b) && size[find(a)] <= adj[x].size()) {
        continue;
    }

原作者的说明、完整代码：总体框架为贪心，即尽量把小数字放在编号小的节点。

假设节点 (x) 上的数字沿着路径 (x -> p1 -> p2 -> ... -> pk -> y) 最终到达了节点 (y)，那么有三个条件需要满足：

((x, p1)) 为所有与节点 (x) 相连的边中最早被删除的 ((pk, y)) 为所有与节点 (y) 相连的边中最晚被删除的对于上述路径上的任意中间节点 (pi)，路径中与该节点有关的两条边一定在所有与该节点相连的边中被连续删除对于单个节点 (x)，我们将所有与之相连的边视作特殊节点，那么上述三个条件分别对应特殊节点构成的图上的“标记起始点”、“标记终点”、“连有向边”三种操作。最终每个节点对应的特殊节点构成的图应满足：

由若干条链组成
无连入至起始点的边
无由终点连出的边
在每次 dfs 暴力寻找编号最小的可行节点时，特殊节点构成的图的合法性可以通过并查集和节点的出/入度来检验。

实现代码时需要注意的细节较多，可以通过为每一个节点额外建立一个虚特殊节点来减少使用并查集时特殊情况的判断。注意特判 (n = 1) 的情况，否则会无法通过 UOJ 的 Extra Test（尽管官方数据并没有这种情况）。

#include <vector>
#include <cstdio>
#include <iostream>
#include <cstring>

using std::cin;
using std::cout;
using std::ios;
using std::vector;

const int N = 2000;

int n, p, id_cnt, a[N], id[N][N], father[N], size[N], degree[N][2]; // 0: in, 1: out
vector<int> adj[N], pool, path;
bool used[N];

int find(int x) { return father[x] == x ? x : father[x] = find(father[x]); }

void merge(int x, int y) { // x->y
  ++degree[x][1];
  ++degree[y][0];
  x = find(x);
  y = find(y);
  father[x] = y;
  size[y] += size[x];
}

void dfs(int x, int f) {
  if (x != f && !used[x]) {
    int y = id[x][f];
    bool legal = true;
    if (degree[x][0] || degree[y][1]) {
      legal = false;
    }
    if (find(x) == find(y) && size[find(x)] <= adj[x].size()) {
      legal = false;
    }
    if (legal) {
      p = std::min(p, x);
    }
  }
  for (auto y : adj[x]) {
    if (y != f) {
      int a = x == f ? x : id[x][f], b = id[x][y];
      if (degree[b][0] || degree[a][1]) {
        continue;
      }
      if (find(a) == find(b) && size[find(a)] <= adj[x].size()) {
        continue;
      }
      dfs(y, x);
    }
  }
}

void dfs_path(int x, int goal, int f = 0) {
  pool.push_back(x);
  if (x == goal) {
    path = pool;
    return;
  }
  for (auto y : adj[x]) {
    if (y != f) {
      dfs_path(y, goal, x);
    }
  }
  pool.pop_back();
}

int get(int x) {
  p = n + 1;
  dfs(x, x);
  used[p] = true;
  pool.clear();
  dfs_path(x, p);
  int m = path.size();
  merge(path[0], id[path[0]][path[1]]);
  for (int i = 0; i + 2 < m; ++i) {
    int a = path[i], b = path[i + 1], c = path[i + 2];
    merge(id[b][a], id[b][c]);
  }
  merge(id[path[m - 1]][path[m - 2]], path[m - 1]);
  return p;
}

int main() {
  freopen("tree.in", "r", stdin);
  freopen("tree.out", "w", stdout);
  ios::sync_with_stdio(false);
  cin.tie(0);
  int tt;
  cin >> tt;
  while (tt--) {
    cin >> n;
    for (int i = 1; i <= n; ++i) {
      cin >> a[i];
    }
    if (n == 1) {
      cout << 1 << '\n';
      continue;
    }
    for (int i = 1; i <= n; ++i) {
      adj[i].clear();
    }
    for (int i = 1; i < n; ++i) {
      int x, y;
      cin >> x >> y;
      adj[x].push_back(y);
      adj[y].push_back(x);
    }
    id_cnt = n;
    for (int i = 1; i <= n; ++i) {
      for (auto j : adj[i]) {
        id[i][j] = ++id_cnt;
      }
    }
    for (int i = 1; i <= id_cnt; ++i) {
      father[i] = i;
      size[i] = 1;
    }
    memset(used, false, sizeof used);
    memset(degree, 0, sizeof degree);
    for (int i = 1; i <= n; ++i) {
      cout << get(a[i]) << " \n"[i == n];
    }
  }
  return 0;
}